Image Classification
Challenges
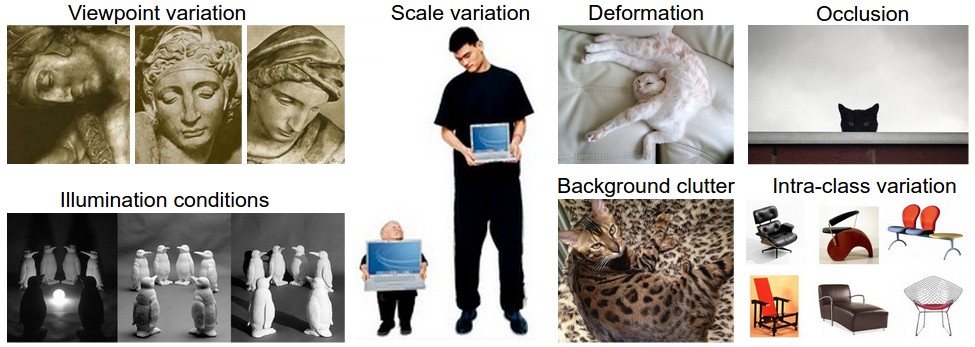
- Viewpoint variation. A single instance of an object can be oriented in many ways with respect to the camera.
- Scale variation. Visual classes often exhibit variation in their size (size in the real world, not only in terms of their extent in the image).
- Deformation. Many objects of interest are not rigid bodies and can be deformed in extreme ways.
- Occlusion. The objects of interest can be occluded. Sometimes only a small portion of an object (as little as few pixels) could be visible.
- Illumination conditions. The effects of illumination are drastic on the pixel level.
- Background clutter. The objects of interest may blend into their environment, making them hard to identify.
- Intra-class variation. The classes of interest can often be relatively broad, such as chair. There are many different types of these objects, each with their own appearance.
Data-Driven Approach
- first accumulating a training dataset of labeled images
- then develop learning algorithms that look at these examples and learn about the visual appearance of each class
Image Classification Pipeline
- Input: Our input consists of a set of N images, each labeled with one of K different classes. We refer to this data as the training set.
- Learning: Our task is to use the training set to learn what every one of the classes looks like. We refer to this step as training a classifier, or learning a model.
- Evaluation: In the end, we evaluate the quality of the classifier by asking it to predict labels for a new set of images that it has never seen before. We will then compare the true labels of these images to the ones predicted by the classifier. Intuitively, we’re hoping that a lot of the predictions match up with the true answers (which we call the ground truth).
Example Image Classification Dataset: CIFAR-10
- CIFAR-10 dataset
- 60,000 tiny images that are 32 pixels high and wide
- Each image is labeled with one of 10 classes (for example “airplane, automobile, bird, etc”)
- These 60,000 images are partitioned into a training set of 50,000 images and a test set of 10,000 images.
- kaggle leaderboard
kNN

- Hyperparameters:
$k$, distance function - Higher
$k$, variance$\downarrow$(more resistant to outliers), bias$\uparrow$$\Rightarrow$bias-variance tradeoff - L2 distance prefers many medium disagreements to one big one.
- L1 distance: depends on the choice of coordinate system
- if entries of feature vector have important meaning, L1 may be more natural
- kNN demo
Load Data
Xtr_orig, Ytr, Xte_orig, Yte = load_CIFAR10(cifar10_dir) # a magic function we provide
# flatten out all images to be one-dimensional
Xtr = Xtr_orig.reshape(Xtr_orig.shape[0], -1) # Xtr becomes 50000 x 3072
Xte = Xte_orig.reshape(Xte_orig.shape[0], -1) # Xte becomes 10000 x 3072
Train and Evaluate a Classifier
- API
KNearestNeighbour()
knn = KNearestNeighbor() # create a kNN classifier instance
knn.train(Xtr, ytr) # train the classifier on the training images and labels
yte_predict = knn.predict(Xte) # predict labels on the test images
# accuracy = fraction of examples that were correctly predicted
accuracy = np.mean(yte_predict == yte)
print('accuracy: %f' % accuracy)
Implementation of kNN Classifier with L2 Distance
Vectorization of Distance Computation
$$ A = \begin{pmatrix} a_1\newline \vdots\newline a_N \end{pmatrix} \in \mathbb{R}^{N \times D},\ \ B = \begin{pmatrix} b_1\newline \vdots\newline b_M \end{pmatrix} \in \mathbb{R}^{M \times D} $$
$$ E_{ij} = \Vert b_i- a_j\Vert_2, \ \ E=(E_{ij})\in\mathbb{R}^{M\times N} $$
$$ E_{ij}^2=-2b_i a_j^T +\Vert b_i\Vert_2^2 +\Vert a_j\Vert_2^2 =-2 (BA^T)_{ij} +\Vert b_i\Vert_2^2 +\Vert a_j\Vert_2^2 $$
b = np.sum(B * B, axis = 1, keepdims = True)
a = np.sum(A * A, axis = 1, keepdims = True)
E = np.sqrt(-2 * np.dot(B, A.T) + b + a.T) # numpy broadcasting
import numpy as np
from scipy.stats import mode
class KNearestNeighbor(object):
""" a kNN classifier with L2 distance """
def __init__(self):
pass
def train(self, X, y):
"""
X: X.shape == (N, D), N examples, each of dim D
y: y.shape == (N,)
y[i] is the label of X[i]
"""
# the nearest neighbor classifier simply remembers all the training data
self.Xtrain = X
self.ytrain = y
def computeDistances(self, X):
"""
Compute the distances between each test point in X
and each training point in self.Xtrain
Input:
X: each row is an example we wish to predict label for
X.shape == (ntest, D)
Output:
dists: dists.shape == (ntest, ntrain)
dists[i, j] == L2 distance between X[i] and self.Xtrain[j]
"""
ntest, ntrain = X.shape[0], self.Xtrain.shape[0]
te = np.sum(X * X, axis = 1, keepdims = True)
tr = np.sum(self.Xtrain * self.Xtrain, axis = 1, keepdims = True)
dists = np.sqrt(-2 * np.dot(X, self.Xtrain.T) + te + tr.T)
def predict(self, X, k = 1):
"""
Predict labels for test data using this classifier.
Input:
X: each row is an example we wish to predict label for
X.shape == (ntest, D)
Output:
ypred: ypred.shape == (ntest,)
ypred[i] is the predicted label for X[i]
"""
dists = self.computeDistances(X)
ntest = X.shape[0]
# ith row: indices of k nearest neighbors of X[i]
k_idx = dists.argsort(axis = 1)[:, :k]
# ith row: labels of k nearest neighbors of X[i]
closest_y = self.ytrain[k_idx]
# ith row: most common label in closest_y[i]
y_pred = mode(closest_y, axis = 1).mode
return np.squeeze(y_pred)
Hyperparameter Tuning
- Validation Set (50%-90% for training, rest for validation)
- Cross Validation
- in practice, tend to avoid CV since CV can be computationally expensive
- typical # of folds: 3, 5, 10
- If the # of hyperparameters is large you may prefer to use bigger validation splits
- If the # of examples in the validation set is small (perhaps only a few hundred or so), it is safer to use CV
Evaluate on the test set only a single time, at the very end.
Split your training set into training set and a validation set. Use validation set to tune all hyperparameters. At the end run a single time on the test set and report performance.
Pros and Cons of kNN
With $N$examples, how fast are training and prediction?
- Training:
$O(1)$, only need to memorize training data - Prediction:
$O(N)$, need to compare test example to each of the sample in the training set - in practice, we want classifiers that are fast at prediction; slow for training is ok
Approximate Nearest Neighbor (ANN) algorithms (e.g. FLANN)
- accelerate the NN lookup
- trade off the correctness of the nearest neighbor retrieval with its space/time complexity during retrieval
- rely on a pre-processing/indexing stage that involves building a KDtree, or running the k-means algorithm
Python Code
kNN in Practice (Never Used on Images)
- Normalize the features in your data (e.g. one pixel in images) to have zero mean and unit variance.
- If your data is very high-dimensional, consider using a dimensionality reduction technique such as PCA (wiki ref, CS229ref, blog ref) or even Random Projections.
- Split your training data randomly into train/val splits.
- Train and evaluate the kNN classifier on the validation data (for all folds, if doing cross-validation) for many choices of
$k$and across different distance types. - If your kNN classifier is running too long, consider using an Approximate Nearest Neighbor library (e.g. FLANN) to accelerate the retrieval (at cost of some accuracy).
- Take note of the hyperparameters that gave the best results. There is a question of whether you should use the full training set with the best hyperparameters, since the optimal hyperparameters might change if you were to fold the validation data into your training set (since the size of the data would be larger). In practice it is cleaner to not use the validation data in the final classifier and consider it to be burned on estimating the hyperparameters. Evaluate the best model on the test set. Report the test set accuracy and declare the result to be the performance of the kNN classifier on your data.