How to Improve Learning Algorithms

• get more training examples
• feature selection
• get additional features
• add polynomial features
• decrease/increase $\lambda$

Evaluate a Learning Algorithm

• training/validation/test set, e.g. 60/20/20 split
• training/validation/test error
• model selection:
  1. optimize parameters by minimizing training error for each model
  2. select the model with the least validation error (e.g. select polynomial degree $d$)
• estimate generalization error using test error

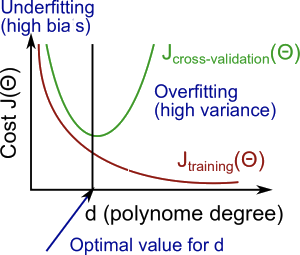
Machine Learning Diagnostic: Bias vs Variance

• can rule out certain courses of action as being unlikely to improve the performance of your learning algorithm significantly
• high bias = underfit = high training error, validation error $\approx$ training error
• high variance = overfit = low training error, validation error $\gg$ training error

Regularization and Bias/Variance

• large $\lambda$ $\Rightarrow$ high bias = underfit
• small $\lambda$ $\Rightarrow$ high variance = overfit
• choose regularization parameter
  1. create a list of $\lambda$s
  2. create a list of models
  3. iterate through the $\lambda$s and for each $\lambda$ go through all the models to optimize parameter $\Theta$
  4. compute validation error using the learned $\Theta$
  5. select the best combo with the least validation error
  6. estimate generalization error using test error

Learning Curves

• as the training set gets larger, the training error increases
• error value will plateau out after a certain training set size
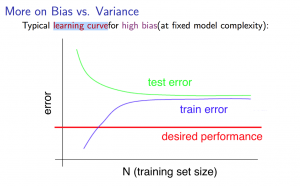
• Experiencing high bias:
  • Low training set size: low training error, high validation error
  • Large training set size: high training error, validation error $\approx$ training error
  • getting more training data will not (by itself) help much

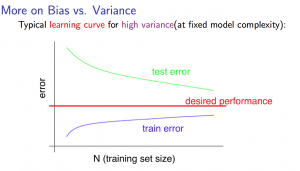
• Experiencing high variance:
  • Low training set size: low training error, high validation error
  • Large training set size: training error increases with training set size, validation error continues to decrease without leveling off; difference between 2 errors remains significant
  • getting more training data is likely to help

Debugging a Learning Algorithm

• get more training examples $\rightarrow$ fit high variance
• feature selection $\rightarrow$ fit high variance
• get additional features $\rightarrow$ fit high bias
• add polynomial features $\rightarrow$ fit high bias
• increase $\lambda$ $\rightarrow$ fit high variance
• decrease $\lambda$ $\rightarrow$ fit high bias

Neural Networks and Overfitting

• small nn
  • fewer parameters
  • more prone to underfitting
  • computationally cheaper
• larger nn
  • more parameters
  • more prone to overfitting
  • computationally expensive
  • use regularization to address overfitting