Model Representation

$$
a_i^{[j]} = \text{“activation” of unit $i$ in layer $j$} \\
\Theta^{[j]} = \text{matrix of weights controlling function mapping from layer $j$ to layer $j+1$}
$$
Forward Propagation: Vectorized Implementation
$$ [x] \rightarrow [a^{[2]}] \rightarrow [a^{[3]}]\rightarrow \cdots $$
- input:
$x$. Setting$a^{[1]}=x$ - linear combination:
$z^{[j]}=\Theta^{[j-1]}a^{[j-1]}, \ \ j=2,3,\ldots$ - activation:
$a^{[j]}=g(z^{[j]}), \ \ j=2,3,\ldots$
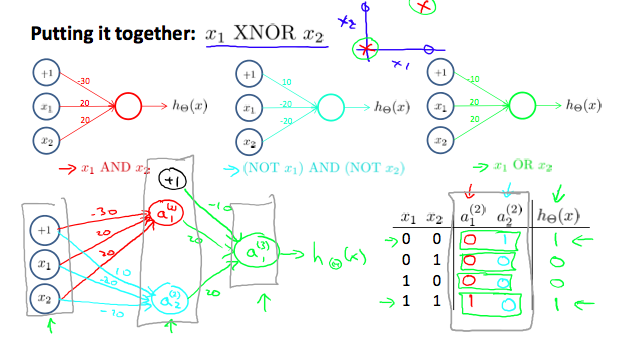
Non-linear Classification Example: XNOR operator
| x1 | x2 | XNOR = NOT XOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- using a hidden layer with two nodes (sigmoid activation function)
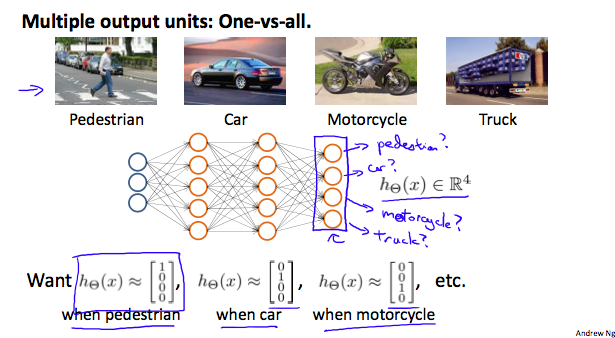
Multiclass Classification
Cost Function
$\{x^{(i)},y^{(i)}\}$,$y\in\mathbb{R}^K$$L$: total # of layers in network$s_{\ell}$: # of neurons in layer$\ell$cost function (generalization of logistic regression cost function)
$$ h_{\Theta}(x)\in\mathbb{R}^K, h_{\Theta}(x)_i = i\text{th output} $$
$$ J(\Theta)=-\frac{1}{N}\sum_{i=1}^N\sum_{k=1}^K\left[ y_{k}^{(i)}\log h_{\Theta}(x^{(i)})_k + (1-y_{k}^{(i)})\log (1-h_{\Theta}(x^{(i)})_k) \right]+ \frac{\lambda}{2N}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_{l+1}}(\Theta_{ji}^{(l)})^2 $$
Back Propagation
min $J(\Theta)$, need to compute
$J(\Theta)$$\frac{\partial}{\partial\Theta}J(\Theta)$
Given one training example $(x,y)$:
Forward Propagation
Single training example: $$ \begin{aligned} a^{[1]}&=x \ (\text{add } a^{[1]}_0)\newline z^{[\ell]}&=\Theta^{[\ell-1]}a^{[\ell-1]},\ a^{[\ell]}=g(z^{[\ell]}) \ (\text{add } a^{[\ell]}_0), L=2,3,\ldots,L-1\newline z^{[L]}&=\Theta^{[L-1]}a^{[L-1]},\ a^{[L]}=h_{\Theta}(x)=\sigma(z^{[L]}) \end{aligned} $$
$N$training examples: $$ X = \begin{pmatrix} x^{(1)T}\newline x^{(2)T}\newline \vdots\newline x^{(N)T} \end{pmatrix} $$$$ \begin{aligned} A^{[1]}&=\left[\textbf{1}\ X\right] \newline Z^{[\ell]}&=A^{[\ell-1]}\Theta^{[\ell-1]T},\ A^{[\ell]}=\left[\textbf{1}\ g(Z^{[\ell]})\right] , L=2,3,\ldots,L-1\newline Z^{[L]}&=A^{[L-1]}\Theta^{[L-1]T},\ A^{[L]}=h_{\Theta}(X)=\sigma(Z^{[L]}) \end{aligned} $$
Backward Propagation
Single training example:
$\delta_{j}^{[\ell]}=$“error” of node$j$in layer$\ell = \frac{\partial J}{\partial z_j^{[\ell]}}$$\delta^{[L]}=a^{[L]}-y$$$ \begin{aligned} J &= -y^T\log(a^{[L]}) - (1-y)^T\log (1-a^{[L]})\newline \Rightarrow \frac{\partial J}{\partial a^{[L]}_j} &=-\frac{y_j}{a^{[L]}_j} - \frac{1-y_j}{1-a^{[L]}_j}\newline \Rightarrow \frac{\partial J}{\partial z_j^{[\ell]}} &= \frac{\partial J}{\partial a^{[L]}_j}\frac{d a^{[L]}_j}{dz^{[L]}_j}= \left(-\frac{y_j}{a^{[L]}_j} - \frac{1-y_j}{1-a^{[L]}_j} \right)a^{[L]}_j(1-a^{[L]}_j)=a^{[L]}_j-y_j\newline \Rightarrow \frac{\partial J}{\partial z^{[L]}}&=a^{[L]}-y \end{aligned} $$
$\delta^{[\ell]}=(\tilde{\Theta}^{[\ell]})^T\delta^{[\ell+1]}*g'(z^{[\ell]}), \ \ \ell=L-1,\ldots,2$and$\tilde{\Theta}=\Theta$without the first columnchain rule of vector derivative $$ \begin{aligned} \delta^{[\ell]}&=\frac{\partial J}{\partial z^{[\ell]}}\newline &=\frac{\partial a^{[\ell]}}{\partial z^{[\ell]}} \frac{\partial z^{[\ell+1]}}{\partial a^{[\ell]}} \frac{\partial J}{\partial z^{[\ell+1]}}\newline &=\frac{\partial a^{[\ell]}}{\partial z^{[\ell]}} (\tilde{\Theta}^{[\ell]})^T \delta^{[\ell+1]} \end{aligned}, $$
$$ \frac{\partial a^{[\ell]}}{\partial z^{[\ell]}}=diag\{g’(z^{[\ell]}_1), g’(z^{[\ell]}_2),\ldots,g’(z^{[\ell]}_{s_l})\}, $$
$$ \begin{aligned} \Rightarrow \delta^{[\ell]} &=diag\{g’(z^{[\ell]}_1), g’(z^{[\ell]}_2),\ldots,g’(z^{[\ell]}_{s_l})\} (\tilde{\Theta}^{[\ell]})^T \delta^{[\ell+1]}\newline &= (\tilde{\Theta}^{[\ell]})^T \delta^{[\ell+1]} * g’(z^{[\ell]}) \text{ (element-wise multiplication)} \end{aligned} $$
- unregularized case:
$ \frac{\partial J}{\partial\Theta^{[\ell]}}=\delta^{[\ell+1]}(a^{[\ell]})^T$$$ \begin{aligned} \frac{\partial J}{\partial \Theta^{[\ell]}_{ij}}&=\frac{\partial J}{\partial z^{[\ell+1]}_i}\frac{\partial z^{[\ell+1]}_i}{\partial \Theta^{[\ell]}_{ij}}\newline &=\delta^{[\ell+1]}_i a^{[\ell]}_j \end{aligned} $$
$$ \Rightarrow \frac{\partial J}{\partial\Theta^{[\ell]}}=\delta^{[\ell+1]}a^{[\ell]T} $$
$N$training examples: VECTORIZATION
$\Delta^{[L]}=A^{[L]}-Y$
$\Delta^{[\ell]}=\Delta^{[\ell+1]}\tilde{\Theta}^{[\ell]}*g'(Z^{[\ell]}), \ \ \ell=L-1,\ldots,2$Gradient of
$\Theta^{[\ell]}$:$$ D^{[\ell]}=\frac{1}{N}\Delta^{[\ell+1]T}A^{[\ell]}+\frac{\lambda}{N}\hat{\Theta}^{[\ell]},\text{ where } \hat{\Theta}^{[\ell]}=\Theta^{[\ell]} \text{ with first column being all 0} $$