Logistic Regression Model

• goal: want $h_{\theta}(x) \in [0,1]$
• $h_{\theta}(x)=g(\theta^Tx)$, where $g(z)=\frac{1}{1+e^{-z}}$ (sigmoid function/ logistic function)
• interpretations: $h_{\theta}(x)$ = estimated probability that $y=1$ on input $x$, that is

$$h(x)=h_{\theta}(x) = \Pr(y=1|x;\theta)$$

• prediction: predict $y=1$ if $h_{\theta}(x)\geq 0.5 \Leftrightarrow \theta^Tx\geq 0$

• Decision Boundary: $\theta^Tx= 0$

• Nonlinear Decision Boundary: add complex (i.e. polynomial) terms

• Notations: training set $\{(x^{(i)}, y^{(i)})\}_{i=1}^N$, where

$$ x = \begin{pmatrix}x_0\newline x_1\newline\vdots\newline x_p\end{pmatrix}\in\mathbb{R}^{p+1}, x_0=1,y\in\{0,1\} $$

Logistic Regression Cost/ Loss Function

$$ J(\theta)=\frac{1}{N}\sum_{i=1}^N L\left(h(x^{(i)}),y^{(i)}\right), \text{where} $$

$$ L(h(x), y)=\begin{cases} -\log h(x), &y=1\newline -\log(1-h(x)), &y=0 \end{cases} $$

$$ \Rightarrow L(h(x), y)=-y\log h(x)-(1-y)\log(1-h(x))=-log\left[h(x)^y (1-h(x))^{1-y}\right] $$

• interpretation of cost function:
  1. if $h(x)=y$ for $y=1$ or $0$, then $L(h(x), y)=0$
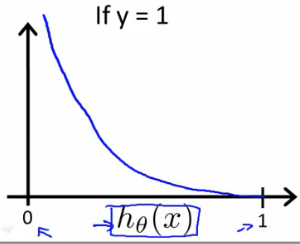
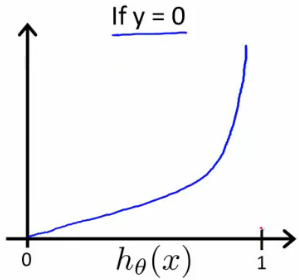
  2. if $y=1$, $L(h(x), y)\rightarrow\infty$ as $h(x)\rightarrow 0$
  3. if $y=0$, $L(h(x), y)\rightarrow\infty$ as $h(x)\rightarrow 1$

• why not quadratic loss?
  • To ensure convexity (Left: quadratic loss, Right: logistic loss)
  • Maximum Likelihood Estimation

Gradient Descent

$$ \frac{\partial}{\partial\theta_j}J(\theta) = \frac{1}{N} \sum_{i=1}^N \frac{\partial}{\partial\theta_j}L(h(x^{(i)}),y^{(i)}) $$

Let $z = \theta^T x, a=h_{\theta}(x)=sigmoid(z)$, then $$ \frac{\partial L}{\partial\theta_j}=\frac{\partial L}{\partial a}\frac{\partial a}{\partial z}\frac{\partial z}{\partial\theta_j}\\
\Rightarrow \frac{\partial L}{\partial a} = -\frac{y}{a}+\frac{1-y}{1-a},\ \ \ \frac{\partial a}{\partial z}=a(1-a), \ \ \ \frac{\partial z}{\partial\theta_j}=x_j\\
\Rightarrow \frac{\partial L}{\partial\theta_j}=(a-y)x_j=(h(x)-y)x_j $$

Algorithm:

repeat{

$\theta_j \leftarrow \theta_j -\alpha\frac{\partial}{\partial \theta_j}J(\mathbf{\theta})=\theta_j -\alpha\frac{1}{N}\sum _{i=1}^N \left(h(x^{(i)}) - y^{(i)}\right)x^{(i)}_j$

} (simultaneously update for $j=0,1,...,p$)

$\alpha$: learning rate (step size)

Vectorization

$$ \theta \leftarrow \theta-\frac{\alpha}{N} X^T (h(X)-y) $$

def sigmoid(u):
    return 1/(1 + np.exp(-u))

# X: design matrix, N*(p+1)
# Y: N*1
# theta: (p+1)*1

# compute hypothesis
h = sigmoid(np.dot(theta.T, X))

# compute cost
J = - np.mean(np.log(h) * Y +  np.log(1-h) * (1-Y))

# compute descent
N = X.shape[0]
dtheta = np.dot(X.T, h - Y)/N

# update params
theta -= learning_rate*dtheta

Advanced Optimization Methods

• Algorithms:
  • conjugate gradient
  • BFGS
  • L-BFGS
• Advantages:
  • no need to manually pick learning rate (step size) $\alpha$
  • often faster than gradient descent
• Disadvantages:
  • more complex

Multiclass Classification: One-vs-All

• $K$ classes, fit $K$ classifiers: $$ h^{(k)}_{\theta}(x)=\Pr(y=i|x;\theta),\ \ \ \ k=1,2,\ldots,K. $$

$$ x \rightarrow \text{class } k^*=\arg\max_{k=1,2\ldots,K} h^{(k)}_{\theta}(x) $$

Solving the Problem of Overfitting

• underfitting: high bias
• overfitting: high variance
• address overfitting:
  1. reduce # of features:
     • manually select
     • model selection algorithm
  2. regularization:
     • keep all the features, but reduce the magnitude of parameters $\theta_j$
     • regularization works well when we have a lot of slightly useful features
• regularization: small values for parameters
  • simpler hypothesis
  • less prone to overfitting

Regularized Linear Regression

$$ J(\theta)=\frac{1}{2N}\left(\sum_{i=1}^N (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda\sum_{j=1}^p \theta_j^2\right) $$

• regularization term: $\lambda\sum_{j=1}^p \theta_j^2$
• regularization parameter: $\lambda\geq 0$
  • Using the above cost function with the extra summation, we can smooth the output of our hypothesis function to reduce overfitting.
  • If $\lambda$ is chosen to be too large, it may smooth out the function too much and cause underfitting.

Gradient Descent

Algorithm:

repeat{

$\theta_0 \leftarrow \theta_0 -\alpha\frac{\partial}{\partial \theta_0}J(\mathbf{\theta})=\theta_j -\alpha\frac{1}{N}\sum _{i=1}^N \left(h(x^{(i)}) - y^{(i)}\right)$

$\theta_j \leftarrow \theta_j -\alpha\frac{\partial}{\partial \theta_j}J(\mathbf{\theta})=\theta_j -\frac{\alpha}{N}\left[\sum _{i=1}^N \left(h(x^{(i)}) - y^{(i)}\right)x^{(i)}_j+\lambda\theta_j\right],\ \ \ \ j=1,...,p$

} (simultaneously update)

$\alpha$: learning rate (step size)

$$\theta_j \leftarrow \left(1-\alpha\frac{\lambda}{N}\right)\theta_j -\alpha\frac{1}{N}\sum _{i=1}^N \left(h(x^{(i)}) - y^{(i)}\right)x^{(i)}_j\ \ \ \ j=1,…,p$$

• $\left(1-\alpha\frac{\lambda}{N}\right) <1$, shrinking

Normal Equation

$$ 2NJ(\theta) =(X\theta-y)^T(X\theta-y) +\lambda \theta^TH\theta, \ \ \ \text{where}\\
H = \begin{pmatrix} 0 &0 &\cdots &0\newline 0 &1 &\cdots &0\newline \vdots &\vdots &\ddots &\vdots\newline 0 &0 &\cdots &1 \end{pmatrix}_{(p+1)\times(p+1)} $$

$$ \Rightarrow N\frac{\partial J}{\partial\theta}=X^TX\theta-X^Ty+\lambda H\theta $$

$$ \Rightarrow \theta^* = (X^TX +\lambda H)^{-1}X^Ty $$

• if $\lambda>0$, $X^TX+\lambda H$ is invertible even when $p>N$.

Regularized Logistic Regression

$$ J(\theta)=-\frac{1}{N}\sum_{i=1}^N\left[y^{(i)}\log h(x^{(i)}) + (1-y^{(i)})\log\left (1-h(x^{(i)})\right)\right] + \frac{\lambda}{2N}\sum_{j=1}^p \theta_j^2 $$

Algorithm:

repeat{

$\theta_0 \leftarrow \theta_0 -\alpha\frac{\partial}{\partial \theta_0}J(\mathbf{\theta})=\theta_j -\alpha\frac{1}{N}\sum _{i=1}^N \left(h(x^{(i)}) - y^{(i)}\right)$

$\theta_j \leftarrow \theta_j -\alpha\frac{\partial}{\partial \theta_j}J(\mathbf{\theta})=\theta_j -\frac{\alpha}{N}\left[\sum _{i=1}^N \left(h(x^{(i)}) - y^{(i)}\right)x^{(i)}_j+\lambda\theta_j\right],\ \ \ \ j=1,...,p$

} (simultaneously update)

$\alpha$: learning rate (step size)

$$ \theta_j \leftarrow \left(1-\alpha\frac{\lambda}{N}\right)\theta_j -\alpha\frac{1}{N}\sum_{i=1}^N \left(h(x^{(i)}) - y^{(i)}\right)x^{(i)}_j,\ \ \ \ j=1,…,p $$

Code in Python

• Logistic Regression: jupyter notebook
• Regularized Logistic Regression: jupyter notebook
• Multiclass Classification with Regularized Logistic Regression-Handwritten Digits Recognition: jupyter notebook